Kapilarne značilnosti in primer v vodi
The kapilarnost Je lastnost tekočin, ki jim omogočajo, da se premikajo skozi cevaste luknje ali porozne površine celo proti sili težnosti. Za to mora obstajati ravnotežje in koordinacija dveh sil, povezanih s tekočimi molekulami: kohezija in adhezija; imata ti dve fizični odsev, imenovan površinska napetost.
Tekočina mora biti zmožna mokre notranje stene cevi ali pore materiala, skozi katerega se premika. To se zgodi, ko je sila adhezije (tekočinska stena kapilarne cevi) večja od sile medpolne kohezije. Posledično tekoče molekule ustvarjajo močnejše interakcije z atomi materiala (steklo, papir itd.) Kot med njimi.
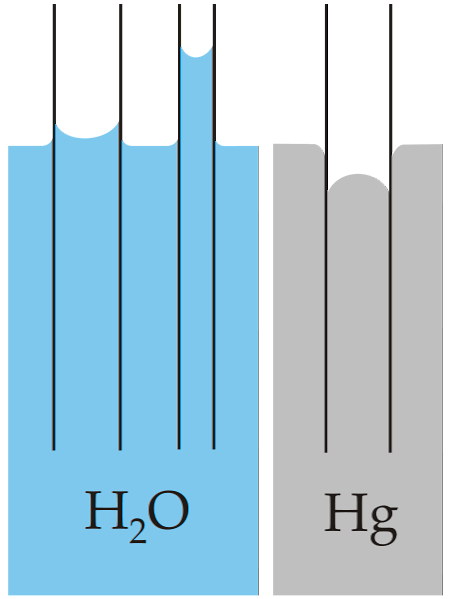
Klasičen primer kapilarnosti je prikazan v primerjavi te lastnosti za dve zelo različni tekočini: vodo in živo srebro.
Zgornja slika kaže, da voda narašča skozi stene cevi, kar pomeni, da ima višje adhezivne sile; medtem ko se nasprotno dogaja z živim srebrom, ker njegove kohezivne, kovinske sile spajanja preprečujejo, da bi steklo zmočilo.
Zato voda tvori konkavni menisk, živo srebro pa konveksni menisk (v obliki kupole). Upoštevati je treba tudi, da je manjši polmer cevi ali odseka, po katerem se tekočina premika, večja je višina ali prevožena razdalja (primerjajte višine vodnih stebrov za obe cevi)..
Indeks
- 1 Značilnosti kapilarnosti
- 1.1 - Površina tekočine
- 1.2 -Višina
- 1.3 - Površinska napetost
- 1.4 - Radar kapilar ali por, kjer se tekočina dvigne
- 1,5 - kontaktni kot (θ)
- 2 Kapilarnost vode
- 2.1 O rastlinah
- 3 Reference
Značilnosti kapilarnosti
-Površina tekočine
Površina tekočine, kar pomeni voda, v kapilari je konkavna; menisk je vbočen. To se zgodi zato, ker je posledica sile, ki deluje na molekule vode v bližini stene cevi, usmerjena proti temu.
V vseh meniskusih obstaja kontaktni kot (θ), ki je kot, ki tvori steno kapilarne cevi s črto, ki se dotika površine tekočine na točki dotika.
Sile adhezije in kohezije
Če adhezijska sila tekočine na kapilarno steno prevlada nad intermolekularno kohezijsko silo, potem je kot θ < 90º; el líquido moja la pared capilar y el agua asciende por el capilar, observándose el fenómeno conocido como capilaridad.
Ko je kapljica vode postavljena na površino čistega stekla, se voda razširi na steklo, tako da je θ = 0 in cos θ = 1.
Če medmolekularna kohezijska sila prevladuje nad adhezijsko trdnostjo kapilarne tekočine na steni, na primer pri živem srebru, bo meniskus konveksen in kot θ ima vrednost> 90 °; živo srebro ne mokri stene kapilare in se zato spušča skozi njeno notranjo steno.
Ko je kapljica živega srebra postavljena na površino čistega stekla, padec ohrani svojo obliko in kot θ = 140º.
-Višina
Voda se dvigne skozi kapilarno cev, da doseže višino (h), v kateri teža vodnega stebra kompenzira vertikalno komponento medmolekularne kohezijske sile.
Ko se bo več vode dvigalo, bo prišlo do točke, kjer bo gravitacija ustavila njegovo dvigovanje, tudi če površinska napetost deluje v vašo korist.
Ko se to zgodi, se molekule ne morejo še naprej vzpenjati po notranjih stenah in vse fizične sile so izenačene. Po eni strani imate sile, ki spodbujajo vzpon vode, po drugi strani pa jo lastna teža potiska navzdol.
Jurinov zakon
To lahko matematično zapišemo na naslednji način:
2 π rΥcosθ = ρgπr2h
Kjer je leva stran enačbe odvisna od površinske napetosti, katere velikost je povezana tudi s kohezijskimi ali medmolekularnimi silami; Cosθ predstavlja kontaktni kot in r polmer luknje, skozi katero se tekočina dviguje.
Na desni strani enačbe imamo višino h, silo teže g in gostoto tekočine; to bi bila voda.
Čiščenje potem imate h
h = (2Υcosθ / ρgr)
Ta formulacija je znana kot Jurinov zakon, ki določa višino, ki jo doseže stolpec tekočine, v kapilarni cevi, ko je teža kolone tekočine uravnotežena s silo vzpona po kapilarnosti.
-Površinska napetost
Voda je dipolarna molekula zaradi elektronegativnosti atoma kisika in njegove molekularne geometrije. To povzroči, da je del molekule vode, kjer se nahaja kisik, negativno nabit, medtem ko je del molekule vode, ki vsebuje 2 vodikova atoma, pozitivno nabit..
Molekule v tekočini medsebojno delujejo zaradi tega prek več vodikovih vezi, ki jih držijo skupaj. Vendar pa so molekule vode, ki se nahajajo v vmesni vodi: zrak (površina), izpostavljene neto privlačnosti molekul tekočega sinusa, ki niso kompenzirane s šibko privlačnostjo z molekulami zraka..
Zato so molekule vode vmesnika izpostavljene privlačni sili, ki skuša odstraniti vodne molekule iz vmesnika; to pomeni, da so vodikovi mostovi, ki so nastali z molekulami v dnu, povlekli tiste, ki so na površini. Tako se površinska napetost skuša zmanjšati površino vmesnika voda: zrak.
Razmerje s h
Če pogledate enačbo Jurinovega zakona, boste ugotovili, da je h neposredno sorazmeren z Υ; zato je večja površinska napetost tekočine, večja je višina, ki lahko naraste skozi kapilaro ali por materiala.
Tako lahko pričakujemo, da se pri dveh tekočinah A in B z različnimi površinskimi napetostmi tista z najvišjo površinsko napetostjo dvigne na višjo višino..
Iz te točke lahko sklepamo, da je visoka površinska napetost najpomembnejša značilnost, ki določa kapilarno lastnost tekočine.
-Polmer kapilare ali por, kjer se tekočina dvigne
Opazovanje Jurinovega zakona kaže, da je višina, ki jo doseže tekočina v kapilari ali por, obratno sorazmerna s polmerom istega.
Čim manjši je polmer, večja je višina, ki jo bo tekočinski stolpec dosegel s kapilarnim delovanjem. To je mogoče videti neposredno na sliki, kjer se voda primerja z živim srebrom.
V stekleni cevi s polmerom polmera 0,05 mm bo vodni stolpec s kapilarnostjo dosegel višino 30 cm. V kapilarnih cevkah s polmerom 1 μm s sesalnim tlakom 1,5 x 103 hPa (ki je enaka 1,5 atm) ustreza izračunu višine vodnega stebra od 14 do 15 m.
To je zelo podobno tistemu, kar se dogaja s temi slamicami, ki se večkrat vrtijo same po sebi. S sesanjem tekočine se ustvari razlika v tlaku, ki povzroči, da se tekočina dvigne do ust.
Največja vrednost višine kolone, dosežene s kapilarnostjo, je teoretična, saj se polmer kapilar ne more zmanjšati nad določeno mejo..
Zakon Poiseuille
To dokazuje, da je tok prave tekočine podan z naslednjim izrazom:
Q = (πr4/ 8ηl) ΔP
Kjer je Q tok tekočine, je njegova viskoznost, l dolžina cevi in ΔP razlika v tlaku.
Pri zmanjševanju polmera kapilare se višina kolone tekočine, ki jo doseže kapilarnost, poveča za nedoločen čas. Vendar pa Poiseuille opozarja, da zmanjšanje polmera prav tako zmanjša pretok tekočine skozi to kapilaro.
Poleg tega bi viskoznost, ki je merilo upora, ki nasprotuje pretoku prave tekočine, še dodatno zmanjšala pretok tekočine..
-Kot kontakta (θ)
Višja kot je vrednost cosθ, višja je višina vodnega stolpca s kapilarnostjo, kot je prikazano v Jurinovem zakonu..
Če je θ majhna in se približuje ničli (0), je cosθ = 1, tako da bo vrednost h največja. Nasprotno, če je θ enako 90 °, cosθ = 0 in vrednost h = 0.
Če je vrednost θ večja od 90 °, kar je v primeru konveksnega meniska, se tekočina ne dvigne s kapilarnostjo in se nagiba, da se spusti (kot se dogaja pri živem srebru).
Kapilarnost vode
Voda ima površinsko napetost 72,75 N / m, relativno visoko v primerjavi z vrednostmi za površinsko napetost naslednjih tekočin:
-Aceton: 22,75 N / m
-Etilni alkohol: 22,75 N / m
-Heksan: 18,43 N / m
-Metanol: 22,61 N / m.
Zato ima voda izjemno površinsko napetost, ki spodbuja razvoj kapilarnega fenomena, ki je tako potreben za absorpcijo vode in hranil v rastlinah..
Na rastlinah

Kapilarnost je pomemben mehanizem za dvig soka s ksilemom rastlin, vendar sam po sebi ni dovolj, da bi sok dosegel liste dreves..
Transpiracija ali izhlapevanje je pomemben mehanizem pri vzponu soka s pomočjo ksilema rastlin. Listi izgubijo vodo z izhlapevanjem, kar povzroči zmanjšanje količine vodnih molekul, kar povzroča privlačnost vodnih molekul, prisotnih v kapilarnih cevkah (ksilem)..
Molekule vode ne delujejo neodvisno druga od druge, ampak delujejo po Van der Waalsovih silah, kar povzroča, da se povežejo s kapilarnimi cevmi rastlin proti listom..
Poleg teh mehanizmov je treba opozoriti, da rastline absorbirajo vodo iz zemlje z osmozo in da pozitivni tlak, ustvarjen v korenu, poganja začetek vzpona vode skozi kapilare rastline..
Reference
- García Franco A. (2010). Površinski pojavi. Vzpostavljeno iz: sc.ehu.es
- Površinski pojavi: površinska napetost in kapilarnost. [PDF] Vzpostavljeno iz: ugr.es
- Wikipedija. (2018). Kapilarnost Vzpostavljeno iz: en.wikipedia.org
- Risvhan T. (s.f.) Kapilarnost v rastlinah. Vzpostavljeno iz: academia.edu
- Helmenstine, Anne Marie, Ph.D. (22. december 2018). Kapilarni ukrep: opredelitev in primeri. Vzpostavljeno iz: thoughtco.com
- Ellen Ellis M. (2018). Kapilarno delovanje vode: definicija in primeri. Študija. Vzpostavljeno iz: study.com
- Osebje ScienceStruck. (16. julij 2017). Primeri, ki pojasnjujejo pojem in pomen kapilarnega delovanja. Vzpostavljeno iz: sciencestruck.com


