Značilnosti heptagonalne prizme in kako izračunati prostornino
A prizemnica je geometrijska figura, ki, kot že ime pove, vključuje dve geometrijski definiciji, ki sta: prizma in heptagon.
"Prizma" je geometrijska figura, omejena z dvema osnovama, ki sta enaka in vzporedna poligona, njihove stranske ploskve pa so paralelogrami..
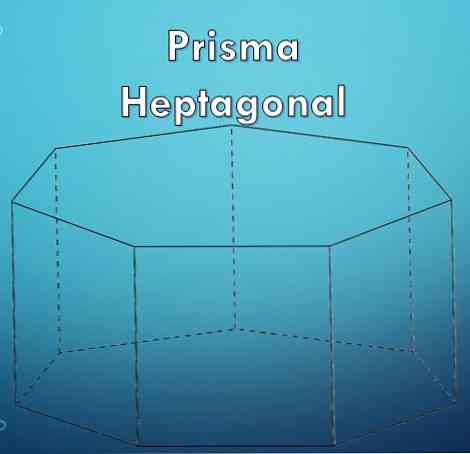
"Šestkotnik" je mnogokotnik, ki ga sestavlja sedem (7) strani. Ker je šesterokotnik mnogokotnik, je lahko reden ali nepravilen.
Poligon pravimo, da je pravilen, če imajo vse njegove strani enako dolžino in so njihovi notranji koti merijo enako, prav tako imenovani so bili enakostranični poligoni; sicer se pravi, da je mnogokotnik nepravilen.

Značilnosti heptagonalne prizme
Sledijo nekatere značilnosti, ki imajo heptagonalno prizmo, kot so: njena konstrukcija, lastnosti njenih podlag, površina vseh obrazov in njena prostornina..
1. Gradnja
Za izgradnjo sedmerokutne prizme sta potrebni dve heptagoni, ki bodo njene osnove in sedem paralelogramov, po ena na vsaki strani šesterokotnika.
Začnite z risanjem šesterokotnika, nato pa narišite sedem navpičnih črt enake dolžine, ki prihajajo iz vsake od njegovih tock.
Nazadnje je še en heptagon sestavljen tako, da njegova vozlišča sovpadajo s koncem črte, ki je bila narisana v prejšnjem koraku.
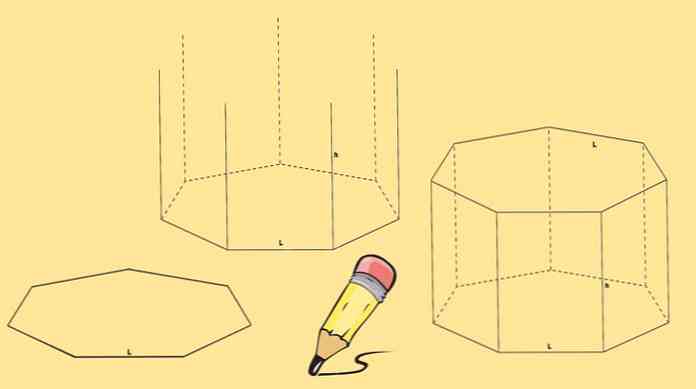
Zgoraj navzgor prikazana heptagonalna prizma se imenuje ravna heptagonalna prizma. Lahko pa imate tudi poševno heptagonalno prizmo, kot je tista na naslednji sliki.

2. Lastnosti njenih baz
Ker so njihove baze heptagoni, ustrezajo, da je diagonalna številka D = nx (n-3) / 2, kjer je "n" število strani mnogokotnika; v tem primeru imamo D = 7 × 4/2 = 14.
Vidimo lahko tudi, da je vsota notranjih kotov katerega koli šesterokotnika (rednega ali nepravilnega) enaka 900 °. To lahko preverite z naslednjo sliko.
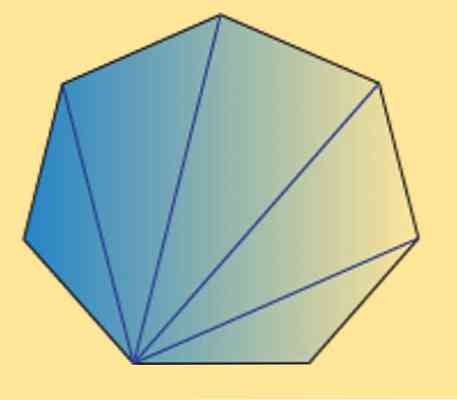
Kot lahko vidite, je 5 notranjih trikotnikov, pri čemer je vsota notranjih kotov trikotnika enaka 180 °, tako da lahko dobimo želeni rezultat..
3. Prostor, potreben za izgradnjo heptagonalne prizme
Ker so njegove osnove dve heptagoni in so njegove strani sedem paralelogramov, je površina, ki je potrebna za konstrukcijo heptagonalne prizme, enaka 2xH + 7xP, kjer je "H" površina vsakega šesterokotnika in "P" območje vsakega paralelograma.
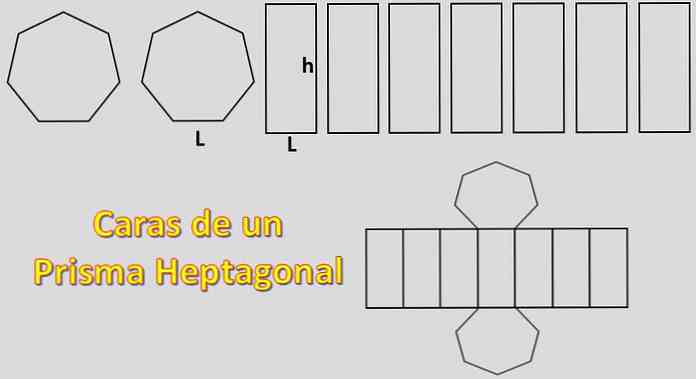
V tem primeru se izračuna površina običajnega šesterokotnika. Za to je pomembno poznati definicijo apotheme.
Apothem je pravokotna linija, ki poteka od središča pravilnega poligona do sredine katerekoli strani.
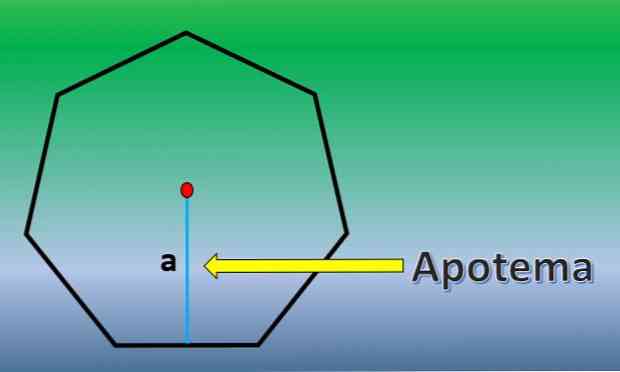
Ko je apotem znan, je območje šesterokotnika H = 7xLxa / 2, kjer je "L" dolžina vsake strani in "a" dolžina apotema..
Območje paralelograma je enostavno izračunati, opredeljeno kot P = Lxh, pri čemer je "L" enaka dolžina strani šesterokotnika in "h" je višina prizme.
Skratka, količina materiala, potrebnega za izgradnjo heptagonalne prizme (z običajnimi bazami) je 7xLxa + 7xLxh, to je 7xL (a + h).
4 - Volumen
Ko je območje baze in višina prizme znano, je volumen določen kot (osnovna površina) x (višina).
V primeru heptagonalne prizme (z običajno osnovo) ima prostornino V = 7xLxaxh / 2; lahko zapišemo tudi kot V = Pxaxh / 2, kjer je "P" obod navadnega šesterokotnika.
Reference
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematika: pristop reševanja problemov za učitelje osnovnega izobraževanja. López Mateos Urejevalci.
- Fregoso, R. S., in Carrera, S. A. (2005). Matematika 3. Uredništvo progreso.
- Gallardo, G., in Pilar, P. M. (2005). Matematika 6. Uredništvo progreso.
- Gutiérrez, C. T., in Cisneros, M. P. (2005). 3. tečaj matematike. Uredništvo progreso.
- Kinsey, L., in Moore, T. E. (2006). Simetrija, oblika in prostor: Uvod v matematiko skozi geometrijo (ponazorjeno, ponatis ed.). Springer znanost in poslovni mediji.
- Mitchell, C. (1999). Dazzling Math Line Designs (Ilustrirana ed.). Scholastic Inc.
- R., M. P. (2005). Narišem 6º. Uredništvo progreso.


