Koliko robov ima heksagonalna prizma?
Vedeti koliko robov ima šesterokotna prizma treba je poznati pomen "roba", "prizme" in "šesterokotnika". Prva dva pojma sta splošni definiciji, tretji koncept pa ima obliko geometrijske figure.
Ko govorimo o šesterokotniku, omenjamo šesterokotnik (poligon). Predpona "hexa" pomeni, da ima mnogokotnik šest strani.

Rob je rob predmeta. Geometrično je črta, ki povezuje dve zaporedni tocki geometrijske figure.
Prizma je geometrijska figura, omejena z dvema vzporednima in enakima poligonomoma in njunima stranskima stranema.
Na naslednji sliki je razvidno, da so lahko stranske površine šesterokotne prizme pravokotniki, lahko pa so tudi paralelogrami..
Glede na vrsto paralelogramov je mogoče premije razvrstiti v dve vrsti: ravne in poševne.
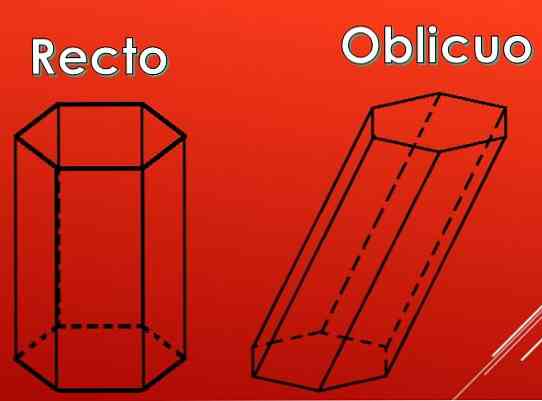
Kako prešteti robove šesterokotne prizme?
Število robov, ki jih bo imela šesterokotna prizma, se ne bo spremenilo, če je ravna ali poševna prizma. Tudi število robov ni odvisno od dolžine stranic.
Štetje robov šesterokotne prizme se lahko izvede na več načinov. Tukaj sta dva načina:
1. Razgradite prizmo
Eden od načinov za štetje robov je razgradnja šesterokotne prizme v dveh osnovah in njenih stranskih straneh. Tako dobimo dva šesterokotnika in paralelogram s petimi notranjimi linijami.
Vsak šesterokotnik ima šest robov, zato ima prizma več kot 12 robov.
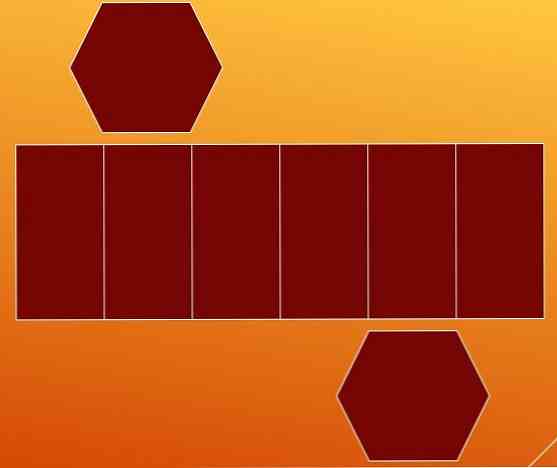
Na prvi pogled velja, da paralelogram vsebuje devet robov (sedem vertikalnih in dveh vodoravnih). Vendar je primerno, da prenehate analizirati ta primer.
Ko je paralelogram upognjen tako, da tvori prizmo, je razvidno, da se bo prva vrstica na levi povezala z zadnjo črto na desni, s katero obe vrstici predstavljata en sam rob..
Kaj pa dve vodoravni črti?
Ko se vsi deli ponovno združijo, se vodoravne črte združijo, vsak s šestimi robovi vsakega šesterokotnika. Zato bi bilo štetje ločeno napaka.
Torej paralelogram vsebuje šest robov prizme, ki skupaj z 12 robovi, štetimi na začetku, daje skupaj 18 robov.
2.- Projiciranje vsakega roba
Drug način, veliko enostavnejši za štetje robov, je uporaba dejstva, da so osnove šesterokotnih prizem šesterokotnikov, nato pa ima vsaka baza šest robov..
Po drugi strani pa se iz vsake tocke šesterokotnika projicira en rob na ustrezno tocko drugega šesterokotnika; to pomeni, da obstaja šest robov, ki se povezujejo z eno bazo.
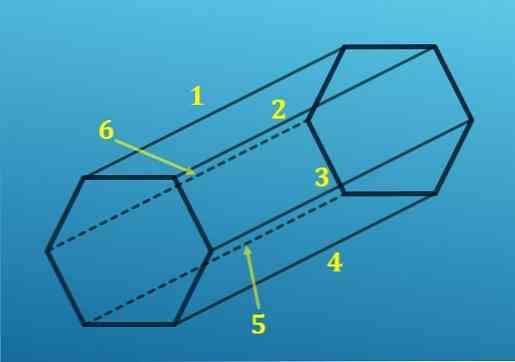
Z dodajanjem vseh robov dobite skupaj 18 robov.
Zaključek
Pokazalo se je, da je število robov prizme enako trikratnemu številu robov, ki jih ima mnogokotnik, ki ga oblikuje..
Zato bo peterokotna prizma imela 3 * 5 = 15 robov, šestkotna prizma bo imela 3 * 7 = 21 robov in se bo lahko uporabila za vsako prizmo.
Reference
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematika: pristop reševanja problemov za učitelje osnovnega izobraževanja. López Mateos Urejevalci.
- Fregoso, R. S., in Carrera, S. A. (2005). Matematika 3. Uredništvo progreso.
- Gallardo, G., in Pilar, P. M. (2005). Matematika 6. Uredništvo progreso.
- Gutiérrez, C. T., in Cisneros, M. P. (2005). 3. tečaj matematike. Uredništvo progreso.
- Kinsey, L., in Moore, T. E. (2006). Simetrija, oblika in prostor: Uvod v matematiko skozi geometrijo (ponazorjeno, ponatis ed.). Springer znanost in poslovni mediji.
- Mitchell, C. (1999). Dazzling Math Line Designs (Ilustrirana ed.). Scholastic Inc.
- R., M. P. (2005). Narišem 6º. Uredništvo progreso.


