Arhimedova biografija, prispevki in izumi
Arhimed iz Sirakuze (287 a.C - 212 a.C) je bil matematik, fizik, izumitelj, inženir in grški astronom iz starodavnega mesta Sirakuze na otoku Siciliji. Njegovi najvidnejši prispevki so Arhimedovo načelo, razvoj metode ekshumacije, mehanska metoda ali oblikovanje prvega planetarija..
Trenutno velja za eno izmed treh pomembnejših osebnosti antične matematike poleg Euklida in Apolonija, saj so njeni prispevki pomenili pomemben znanstveni napredek za čas na področju izračuna, fizike, geometrije in astronomije. Po drugi strani pa je zaradi tega eden najvidnejših znanstvenikov v zgodovini človeštva.

Čeprav je znanih nekaj podrobnosti njegovega osebnega življenja - in tiste, ki so znane, so dvomljive in zanesljive - so njegovi prispevki znani po vrsti pisnih pisem o njegovih delih in dosežkih, ki so se ohranili do danes in pripadajo na dopisovanje, ki ga je hranil leta s prijatelji in drugimi matematiki tistega časa.
Arhimed je bil v svojem času znan po svojih izumih, ki so pritegnili pozornost njegovih sodobnikov, deloma zato, ker so bili uporabljeni kot vojni pripomočki za uspešno preprečevanje številnih rimskih vpadov..
Vendar pa je dejal, da je trdil, da je edina res pomembna stvar matematika in da so bili njegovi izumi le produkt zabave uporabne geometrije. V poznejših letih so bila njegova dela v čisti matematiki veliko bolj cenjena kot njegovi izumi.
Indeks
- 1 Življenjepis
- 1.1 Usposabljanje
- 1.2 Znanstveno delo
- 1.3 Konflikt v Sirakuzah
- 1.4 Smrt
- 2 Znanstveni prispevki Arhimeda
- 2.1 Arhimedovo načelo
- 2.2 Mehanska metoda
- 2.3 Razlaga prava vzvoda
- 2.4 Razvoj metode iztrebljanja ali izčrpavanja za znanstvene predstavitve
- 2.5 Merilo kroga
- 2.6 Geometrija kroglic in valjev
- 3 Izumi
- 3.1 Števec kilometrov
- 3.2 Prvi planetarij
- 3.3 Arhimedov vijak
- 3.4 Arhimedova kremplja
- 4 Reference
Biografija
Arhimed iz Sirakuze se je rodil približno leta 287 pred našim štetjem. O njegovih zgodnjih letih ni znanih veliko informacij, čeprav je mogoče reči, da se je rodil v mestu Syracuse, ki se danes v Italiji šteje za glavno pristanišče otoka Sicilije..
Takrat je bila Sirakuze eno izmed mest, ki so sestavljala tako imenovano Magna Grecia, ki je bila naseljen s naseljenci grškega izvora na južnem delu polotoka v Italiji in na Siciliji..
Ni znanih dejstev o Arhimedovi mami. V zvezi z očetom je znano, da se je to imenovalo Phidias in da je bil posvečen astronomiji. Ta informacija o njegovem očetu je znana po fragmentu knjige Števec peska, je napisal Arhimed, v katerem omenja očetovo ime.
Heraklides, ki je bil grški filozof in astronom, je bil zelo naklonjen Arhimedu in je celo napisal biografijo o njem. Vendar pa ta dokument ni bil ohranjen, zato vse informacije, ki jih vsebuje, niso znane.
Po drugi strani pa je zgodovinar, filozof in biograf Plutarko v svoji knjigi z naslovom Paralelne življenje navedel, da je imel Arhimed krvno zvezo s Hierom II, tiranom, ki je bil v Sirakuzi od leta 265 pr..
Usposabljanje
Zaradi malo informacij, ki jih imamo o Arhimedu, ne vemo zagotovo, kje je dobil svoje prvo usposabljanje.
Vendar pa so različni zgodovinarji ugotovili, da obstaja velika možnost, da je Arhimed študiral v Aleksandriji, ki je bil najpomembnejši grški kulturni in učni center v regiji..
To predpostavko podpirajo podatki grškega zgodovinarja Diodora Sícula, ki je navedel, da je Arhimed verjetno študiral v Aleksandriji..
Poleg tega se v mnogih svojih delih Arhimed sam spomni drugih znanstvenikov časa, katerih delo je bilo skoncentrirano v Aleksandriji, zato se lahko domneva, da se je dejansko razvil v tem mestu..
Nekatere osebnosti, s katerimi naj bi Arhimed medsebojno vplival v Aleksandriji, so geograf, matematik in astronom Eratosten iz Cirene ter matematik in astronom Conon de Sanos.
Družinska motivacija
Po drugi strani pa je lahko dejstvo, da je bil Arhimedov oče astronom, pomembno vplivalo na nagnjenja, ki jih je kasneje pokazal, saj je kasneje in že od mladosti na področju znanosti.
Po njegovem času v Aleksandriji se ocenjuje, da se je Arhimed vrnil v Sirakuze.
Znanstveno delo
Po vrnitvi v Sirakuze je Arhimed začel oblikovati različne artefakte, ki so mu kmalu omogočili določeno priljubljenost med prebivalci tega mesta. V tem obdobju se je popolnoma posvetil znanstvenemu delu, izdelal različne izume in zaključil nekaj matematičnih pojmov, ki so zelo napredovale do svojega časa.
Na primer, ko se je posvetil proučevanju značilnosti trdnih ukrivljenih in ravnih številk, je prišel do konceptov, povezanih z integralnim in diferencialnim računom, ki je bil razvit kasneje..
Tudi Arhimed je bil tisti, ki je opredelil, da volumen, povezan s kroglo, ustreza dvakratni velikosti valja, ki ga vsebuje, in je bil tisti, ki je izumil kompozitni jermen, na podlagi njegovih odkritij o zakonu vzvoda..
Konflikt v Siracusah
V letu 213 pr. N. Št. So rimski vojaki vstopili v mesto Sirakuze in obkrožili svoje naseljenike, da bi se jim predali.
Akcijo so vodili vojaški in grški politik Marco Claudio Marcelo v okviru druge punske vojne. Kasneje je bil znan kot Rimski meč, saj je končal z osvajanjem Sirakuze.
Sredi konflikta, ki je trajal dve leti, so se prebivalci Sirakuze s pogumom in silovitostjo borili proti Rimljanom, Arhimed pa je imel zelo pomembno vlogo, saj se je posvetil ustvarjanju orodij in instrumentov, ki so pomagali premagati Rimljane..
Končno je Marco Claudio Marcelo zavzel mesto Syracuse. Pred veliko Arhimedovo intelektualnostjo je Marcelo ukazal, naj se ne poškodujejo ali ubijejo. Arhimed je bil ubit v rokah rimskega vojaka.
Smrt
Arhimed je umrl leta 212 pr. Več kot 130 let po njegovi smrti, leta 137 pr. N. Št., Je pisatelj, politik in filozof Marco Tulio Cicero zasedel mesto v upravi Rima in želel najti Arhimedovo grobnico..
Ta naloga ni bila lahka, saj Cicero ni mogel najti nikogar, ki bi označil točen kraj. Kljub temu ga je dobil, zelo blizu vrat Agrigenta in v obupnih razmerah.
Ciceron je očistil grobnico in odkril, da je v notranjosti cilindra vpisana krogla, kot sklic na odkritje o obsegu, ki ga je Arhimed pred nekaj časa naredil..
Različice o njegovi smrti
Prva različica
Ena od različic navaja, da je bil Arhimed sredi reševanja matematičnega problema, ko mu je pristopil rimski vojak. Rečeno je, da bi ga Arhimed že nekaj časa prosil za rešitev problema, zato bi ga vojak ubil.
Druga različica
Druga različica je podobna prvi. Račun, da je Arhimed reševal problem matematike, ko je nastopilo mesto.
Rimski vojak je vstopil v njegovo postajo in mu ukazal, naj spozna Marcela, in Arhimed je odgovoril, da mora najprej rešiti problem, na katerem je delal. Vojak se je zaradi tega odgovora razburil in ga ubil.
Tretja različica
Ta hipoteza kaže, da je imel Arhimed v svojih rokah veliko raznolikost instrumentov, značilnih za matematiko. Potem ga je videl vojak in mislil je, da nosi dragocene predmete, zato ga je ubil.
Četrta različica
Ta različica kaže, da se je Arhimed držal pri tleh in razmišljal o načrtih, ki jih je študiral. Očitno je rimski vojak prišel od zadaj in, ne zavedajoč se, da je Arhimed, ga je ustrelil.
Znanstveni prispevki Arhimeda
Načelo Arhimeda
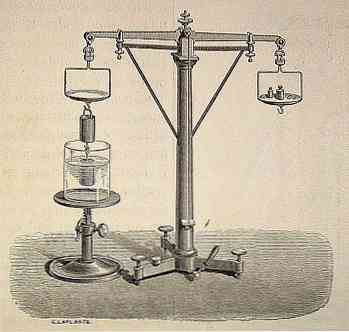
Arhimedovo načelo sodobne znanosti obravnava kot eno od najpomembnejših dediščine antičnega obdobja.
Skozi zgodovino, in ustno, so poročali, da je Arhimed prišel do svojega odkritja po naključju, zahvaljujoč kralju Hieronu, ki je naročil, da ugotovi, ali je bila zlata krona, ki jo je poslal v proizvodnjo, izdelana le zlato. čista in ni vsebovala nobene druge kovine. To sem moral opraviti, ne da bi uničil krono.
Rečeno je, da se je Arhimed meditiral o tem, kako rešiti ta problem, vendar se je odločil, da se kopa, in ko je vstopil v kad, je spoznal, da se je voda povišala, ko se je potopil v to..
Na ta način bi odkril znanstveno načelo, da "vsako telo, ki je v celoti ali delno potopljeno v tekočino (plin ali tekočino), prejme navzgor potisk, ki je enak teži tekočine, ki jo oddaja predmet".
To načelo pomeni, da tekočine povzročajo naraščajočo silo - potiskanje navzgor - na kateri koli predmet, potopljen v njih, in da je količina te potisne sile enaka teži tekočine, ki jo potopljeno telo premakne, ne glede na njegovo težo..
Razlaga tega načela opisuje pojav flotacije in se nahaja v njenem Pogodba o plavajočih telesih.
Arhimedovo načelo je bilo v veliki meri uporabljeno pri splavih za plavanje predmetov masovne rabe, kot so podmornice, ladje, reševalci in baloni..
Mehanska metoda
Drugi najpomembnejši prispevek Arhimeda k znanosti je bila vključitev čisto mehanske, to je tehnične metode v razmišljanje in argumentiranje geometrijskih problemov, kar je pomenilo doslej še nerešen način reševanja te vrste problemov za čas..
V kontekstu Arhimeda je bila geometrija obravnavana kot izključno teoretična znanost, skupno pa je bilo, da se je čista matematika spuščala proti drugim praktičnim znanostim, v katerih bi lahko uporabili svoja načela..
Zato se danes šteje za predhodnico mehanike kot znanstvene discipline.
V pisanju, v katerem matematik izpostavlja novo metodo svojemu prijatelju Eratostenu, to kaže, da to omogoča obravnavo vprašanj matematike preko mehanike, in da je nekoliko lažje zgraditi predstavitev geometrijskega izreka, če je že ima nekaj predhodnega praktičnega znanja, da če nimaš nobene ideje o tem.
Ta nova metoda raziskovanja, ki jo je izvedel Arhimed, bi postala predhodnik neformalne faze odkrivanja in oblikovanja hipotez sodobne znanstvene metode..
Razlaga prava vzvoda
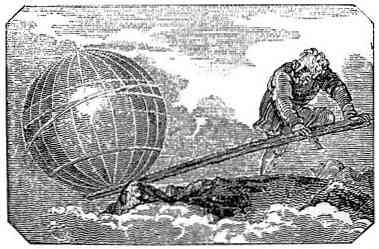
Medtem ko je vzvod preprost stroj, ki je bil uporabljen že mnogo prej kot Arhimed, je bil on tisti, ki je oblikoval načelo, ki pojasnjuje njegovo delovanje v svoji razpravi o ravnotežju ravnin..
Pri oblikovanju tega zakona Arhimed vzpostavlja načela, ki opisujejo različno obnašanje vzvoda pri postavljanju dveh teles nanj, odvisno od njegove teže in oddaljenosti od točke podpore..
Na ta način opozarja, da sta dve telesi, ki ju je mogoče izmeriti (sorazmerno) in sta nameščeni na vzvodu, uravnoteženi, kadar sta na razdalji, obratno sorazmerni s svojo težo..
Na enak način to storijo neizmerna telesa (ki jih ni mogoče izmeriti), toda ta zakon je bil Archimedov dokazljiv samo s telesi prve vrste..
Njegova formulacija principa vzvoda je dober primer uporabe mehanske metode, saj je v skladu z njo pojasnjena v pismu, naslovljenem na Dositeo, ta je bil v prvem trenutku odkrit s pomočjo metod mehanike v praksi.
Kasneje jih je oblikoval z metodami geometrije (teoretično). Iz tega eksperimentiranja na telesih je bil ločen tudi pojem težišča.
Razvoj metode iztrebljanja ali izčrpanja za znanstvene predstavitve
Izčrpanost je metoda, ki se uporablja v geometriji in je sestavljena iz približevanja geometrijskih številk, katerih območje je znano, z napisom in okrajšavo, na drugi, katere območje naj bi bilo znano..
Čeprav Arhimed ni bil ustvarjalec te metode, jo je razvil mojstrsko, s pomočjo katerega je z njo izračunal natančno vrednost Pi.
Arhimed, ki uporablja metodo ekshumacije, napisano in omejeno s šestkotniki na obod premera 1, kar zmanjša na absurdno razliko med površino šestkotnikov in obseg oboda..
Da bi to naredil, je razporedil šestkotnike, ki so tvorili poligone do 16 strani, kot je prikazano na prejšnji sliki.
Na ta način je določil, da je vrednost pi (razmerja med dolžino kroga in njenim premerom) med vrednostmi 3.14084507 ... in 3.14285714 ... .
Arhimed je mojstrsko uporabil metodo exhaución, ker ni le uspel približati izračun vrednosti Pi z nizko stopnjo napake in zato želel, ampak tudi zato, ker je Pi iracionalna številka, s to metodo in dobljenimi rezultati so bili položeni temelji, ki bi kalili v infinitezimalnem računskem sistemu, kasneje pa v sodobnem integralnem računu.
Merilo kroga
Za določitev območja kroga je Arhimed uporabil metodo, ki je sestavljala risanje kvadrata, ki se prilega točno znotraj kroga.
Vedel je, da je območje kvadrata vsota njegovih strani in da je območje kroga večje, in začel delati na približevanju. To je storil tako, da je kvadrat zamenjal s 6-stranskim poligonom in nato delal z bolj zapletenimi poligoni.
Arhimed je bil prvi matematik v zgodovini, ki je pristopil k resnemu izračunu števila Pi.
Geometrija kroglic in valjev
Med devetimi razpravami, ki sestavljajo delo Arhimeda v matematiki in fiziki, obstajajo dve zvezki o geometriji sfer in valjev..
Pričujoče delo obravnava ugotovitev, da je površina polmera polmera štirikrat večja od njegove največje kroge in da je prostornina krogle dve tretjini prostornine valja, v katerega je vgravirana..
Izumi
Števec kilometrov
Znan tudi kot kilometri, je bil izum tega slavnega človeka.
Ta naprava je bila zgrajena na principu kolesa, ki ob obračanju aktivira zobnike, ki omogočajo izračun prevožene razdalje..
V skladu z istim načelom je Arhimed izdelal več tipov odometrov za vojaške in civilne namene.
Prvi planetarij
Na podlagi pričevanja številnih klasičnih pisateljev, kot so Ciceron, Ovid, Claudian, Marciano Capela, Casiodoro, Sexto Empirico in Lactantius, mnogi znanstveniki Arhimedu pripisujejo ustvarjanje prvega osnovnega planetarija..
To je mehanizem, ki ga sestavlja vrsta "sfer", ki so posnemale gibanje planetov. Do sedaj podrobnosti tega mehanizma niso znane.
Po mnenju Cicerona so bili planetariji, ki so jih zgradili Arhimed, dva. V eni od njih sta bili zastopani zemljišče in različni konstelaciji blizu nje.
V drugi, z eno rotacijo, so sonce, luna in planeti opravili svoje samostojne gibe v zvezi s fiksnimi zvezdami na enak način kot v resničnem dnevu. V slednjih se poleg tega lahko opazujejo zaporedne faze in eklipsi lune.
Vijak Arhimeda
Arhimedov vijak je naprava, ki se uporablja za transport vode od spodaj navzgor skozi pobočje, s cevjo ali valjem.
Po grškem zgodovinarju Diodoro je po tem izumu omogočil namakanje rodovitnih zemljišč ob reki Nil v starem Egiptu, saj so tradicionalna orodja zahtevala ogromen fizični napor, ki je izčrpal delavce..
Uporabljeni valj ima v notranjosti vijaka enake dolžine, ki ohranja medsebojno povezan sistem propelerjev ali plavuti, ki opravljajo rotacijsko gibanje, ki ga ročno premika rotacijski vzvod..
Na ta način lahko spirale potisnejo katerokoli snov od spodaj navzgor, tako da tvorijo nekakšno neskončno vezje.
Arhimedova kremplja
Arhimedova kremplja ali železna roka, kot jo poznamo, je bila eno izmed najbolj strašnih vojnih orožij, ki jih je ustvaril ta matematik, ki je postal najbolj pomemben za obrambo rimskih vpadov na Siciliji..
Glede na raziskave, ki so jih izvedli profesorji univerze Drexel Chris Rorres (Oddelek za matematiko) in Harry Harris (Oddelek za gradbeništvo in arhitekturo), je bil velik vzvod, ki je imel ročico, pritrjeno na vzvod z verigo, ki je visela z nje.
Skozi ročico je bila kljuka manipulirana tako, da je padla na sovražno ladjo, cilj pa je bila, da se jo zaskoči in dvigne do te mere, da se lahko ob sprostitvi popolnoma prevrne ali udari po skalah na obali..
Rorres in Harris predstavili na simpoziju "Stroji in izredne strukture antike" (2001), miniaturni prikaz tega artefakta z naslovom "Strašen vojni stroj: Gradnja in delovanje Arhimedove" železne roke "
Za uresničitev tega dela so se oprli na argumente antičnih zgodovinarjev Polibia, Plutarca in Tita Livia..
Reference
- ASSIS, A. (2008). Arhimed, središče gravitacije in prvi zakon mehanike [na spletu]. Dostop do 10. junij 2017 na bourabai.ru.
- DIJKSTERHUIS, E. (1956). Archimedes [na spletu]. Dostopen je 9. junija 2015 na svetovnem spletu: books.google.co.ve/books.
- MOLINA, A. (2008). Raziskovalna metoda Arhimeda iz Sirakuze: intuicija, mehanika in ekshumacija [na spletu]. Dostopen je 10. junija 2017 na svetovnem spletnem produkcijskem centru.
- O'CONNOR, J. & ROBERTSON, R. (1999). Archimedes of Syracuse [na spletu]. Dostopno do 9. junija 2017 na strani history.mcs.st-and.ac.uk.
- PARRA, E. (2009). Arhimed: njegovo življenje, dela in prispevki k sodobni matematiki [na spletu]. Pridobljeno 9. junija 2017 na lfunes.uniandes.edu.co.
- QUINN, L. (2005). Archimedes of Syracuse [na spletu]. Dostopno do 9. junija 2017 na math.ucdenver.edu.
- RORRES, C. in HARRIS, H. (2001). Strašen vojni stroj: Gradnja in delovanje Arhimedove "železne roke" [na spletu]. Pridobljeno 10. junija 2017 na naslovu cs.drexel.edu.
- VITE, L. (2014). Načelo Arhimeda [na spletu]. Vzpostavljeno 10. junija 2017 na naslovu repository.uaeh.edu.mx.


