Koliko osi simetrije ima krog?
The osi simetrije kroga Neskončne so. Te osi so tiste, ki delijo katerokoli geometrijsko obliko na dve natančno enaki polovici.
Krog je sestavljen iz vseh točk, katerih razdalja do fiksne točke je manjša ali enaka določeni vrednosti "r".
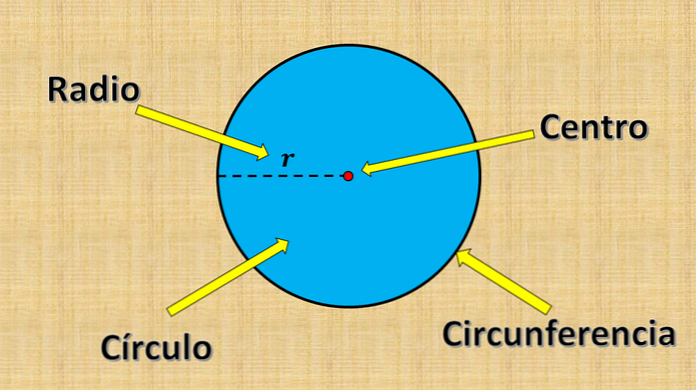
Zgoraj omenjena fiksna točka se imenuje središče, vrednost "r" pa se imenuje polmer. Polmer je največja razdalja med točko na krogu in središčem.
Po drugi strani se vsak odsek črte, katerega konci so na robu kroga (obod) in ki potekajo skozi središče, imenuje premer. Njegova meritev je vedno enaka dvakratnemu polmeru.
Krog in obseg
Ne zamenjujte kroga s krogom. Obod se nanaša samo na točke, ki so na razdalji "r" od središča; to je samo rob kroga.
Toda ko iščete simetrične osi, je ravnodušen, če delate s krogom ali krogom.
Kaj je os simetrije?
Os simetrije je črta, ki na dveh enakih delih deli določeno geometrijsko sliko. Z drugimi besedami, os simetrije deluje kot ogledalo.
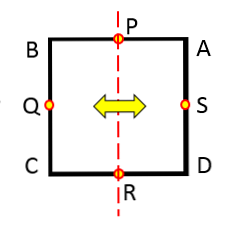
Gredi simetrije kroga
Če opazite kateri koli krog, ne glede na njegov polmer, lahko vidite, da ni vsaka črta, ki prečka, os simetrije..
Na primer, nobena od linij, ki so narisane na naslednji sliki, ni os simetrije.
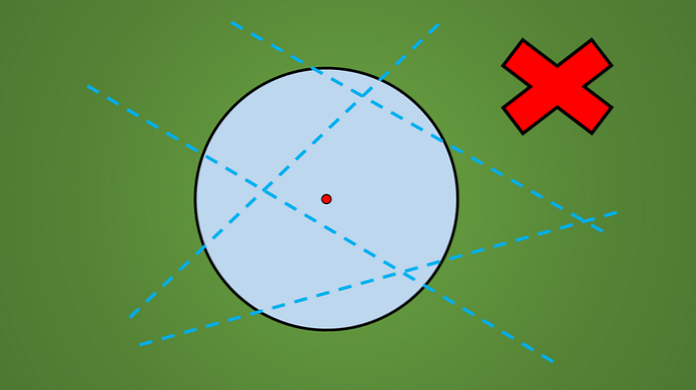
Enostaven način za preverjanje, ali je črta os simetrije ali ne, mora pravokotno odražati geometrično sliko na nasprotni strani črte.
Če odsev ne ustreza prvotni sliki, potem ta linija ni os simetrije. Naslednja slika ponazarja to tehniko.
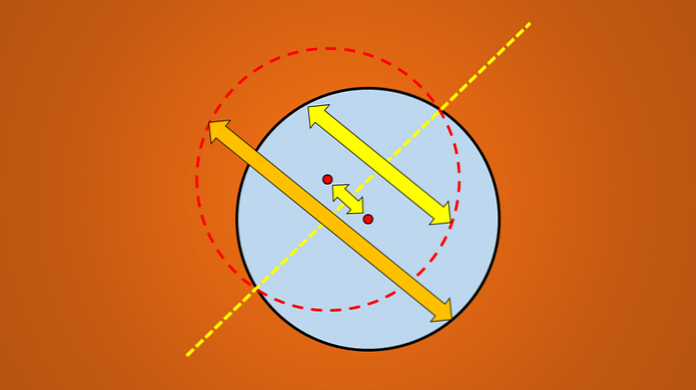
Če pa upoštevamo naslednjo sliko, je dobro znano, da je narisana črta os simetrije kroga.
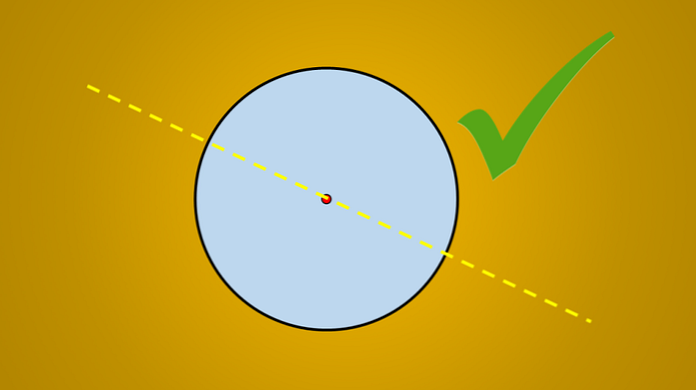
Vprašanje je: ali obstaja več osi simetrije? Odgovor je pritrdilen. Če zavrtite to črto za 45 ° v nasprotni smeri urinega kazalca, je dobljena linija tudi os simetrije kroga.
Enako se zgodi, če zavrtite 90 °, 30 °, 8 ° in na splošno poljubno število stopinj.
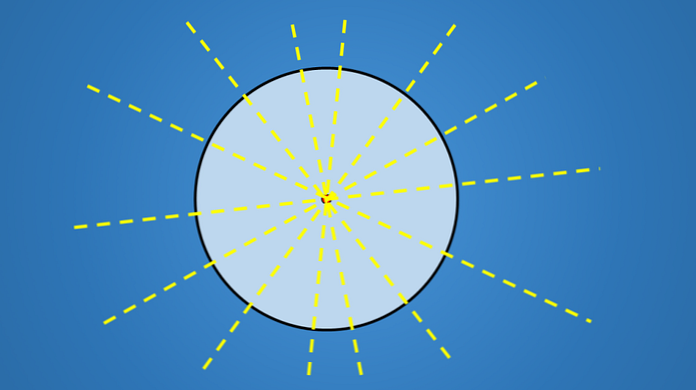
Pomembna stvar pri teh linijah ni nagib, ki ga imajo, ampak vsi gredo skozi središče kroga. Zato je vsaka linija, ki vsebuje premer kroga, os simetrije.
Ker ima krog neskončno število premerov, ima neskončno število simetričnih osi..
Druge geometrijske figure, kot so trikotnik, štirikotnik, peterokotnik, šesterokotnik ali kateri koli drug mnogokotnik, imajo končno število simetričnih osi..
Razlog, zakaj ima krog neskončno število simetrijskih osi, je, da nima nobene strani.
Reference
- Basto, J. R. (2014). Matematika 3: Osnovna analitična geometrija. Patria Editorial Group.
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematika: pristop reševanja problemov za učitelje osnovnega izobraževanja. López Mateos Urejevalci.
- Bult, B., in Hobbs, D. (2001). Matematični leksikon (ilustrirana ed.). (F. P. Cadena, Trad.) Editions AKAL.
- Callejo, I., Aguilera, M., Martinez, L., & Aldea, C. (1986). Matematika Geometrija Reforma zgornjega cikla G.B.. Ministrstvo za šolstvo.
- Schneider, W., & Sappert, D. (1990). Praktični priročnik za tehnično risanje: uvod v osnove industrijskega tehničnega risanja. Reverte.
- Thomas, G. B., & Weir, M. D. (2006). Izračun: več spremenljivk. Pearson Education.


